A Dataset for Visual Navigation with Neuromorphic Methods

Francisco Barranco, Cornelia Fermüller, Yiannis Aloimonos, Tobi Delbruck

Standardized benchmarks for Computer Vision provide very powerful tools for the development of new improved techniques in the field. Currently frame-free event-driven vision still lacks datasets to assess the accuracy of their methods. This dataset provides both frame-free event data and classic image, motion and depth data to assess different event-based methods and compare them to frame-based conventional Computer Vision. We hope that this will help researchers understand the potential of the new technology of event-based vision.

Event-based sensors and frame-based cameras record very different kinds of data streams. Frame-free sensors collect events that are triggered due to changes in the luminance while conventional sensors collect the luminance of the scene. If we want to compare methods for heterogeneous sensors, we will need conventional sensors and frame-free sensors collecting events from the same scene. To do so we used the DAVIS sensor [1] that collects asynchronous events and synchronous frames.

Building a dataset for frame-free sensors

The mechanism to create the dataset for a frame-free sensor consists in collecting events from the frame-free sensor and additional data from cameras, RGB-D sensors (RGB images plus Depth), inertial sensors, or motion capture systems:

• The 3D motion performed by the camera while navigating in the scene can be estimated using a motion capture system [2]. However, accurate motion capture systems are expensive and cannot be used outdoors.
• A stereo rig with a frame-free sensor and a depth sensor also provides the data required for reconstructing the 3D model of the scene. Additionally, a simple odometry system, gyroscope and accelerometer, gives all the required information necessary to estimate the 3D motion and pose ground-truth. We used a robotic platform and a Microsoft Kinect sensor in addition to the DAVIS sensor to create our dataset.

Davis sensor calibration

The DAVIS240b sensor (right in the image) is mounted on a stereo rig together with a Microsoft Kinect Sensor that provides the RGB image and the depth map of the scene. The stereo rig is mounted on a Pan Tilt Unit (PTU-46-17P70T by FLIR Motion Control Systems, left in the image). Finally, the Pan Tilt Unit is on-board a Pioneer 3DX Mobile Robot (center in the image). The PTU controls the pan and tilt angles and angular velocities, while the Pioneer 3DX Mobile Robot is in control of the direction of translation and the speed. There are ROS (Robot Operating System) packages available for the PTU and the Pioneer 3DX mobile robot. Our dataset provides the following:

• The 3D motion parameters: 3D translation of the camera and 3D pose. These are provided by the PTU and the Pioneer Mobile Robot. Assuming that their coordinate centers are the same, they have to be calibrated with respect to the DAVIS coordinates.
• The image depth. It is obtained by the Microsoft Kinect Sensor (RGB-D sensor). A stereo calibration to register the Kinect depth to the DAVIS camera coordinates is required.
• The 2D motion flow field ground-truth. Using the 3D motion parameters and the depth from the DAVIS coordinate system, the 2D motion flow field ground-truth of the scene is reconstructed.

Calibration of DAVIS and RGB-D sensor

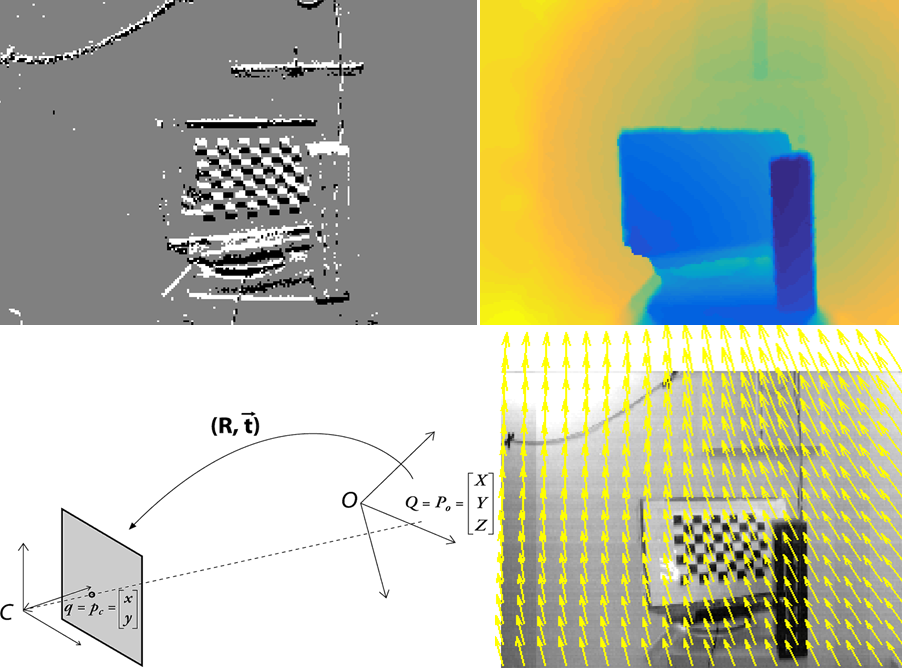
The RGB-D sensor provides the depth of the scene. The RGB data and the Depth in the Kinect sensor are captured by two separate sensors. To obtain the depth rectified with respect to the RGB we use the Kinect SDK. In order to use it in the DAVIS coordinate system, a registration of the depth of the RGB-D sensor is required.

To begin with, we calibrate and extract intrinsic and extrinsic parameters from both DAVIS APS frames and Kinect RGB images. Next, we perform a stereo calibration between the RGB-D sensor and the DAVIS. In other words, the stereo calibration gives us the rotation and translation of the DAVIS with respect to the Kinect.

First, the depth is undistorted using the camera parameters already computed. Next, the 2D coordinates in the image plane are projected into the 3D world coordinates (since the depth is known). The 3D point cloud is then transformed using the rotation and translation computed from the stereo calibration. Last, the new 3D point cloud is projected back into the 2D plane. Now, the new depth registered for the DAVIS coordinate system can be obtained.

Calibration of DAVIS and PTU

The goal is to obtain estimates of the translation and rotation of the camera for a given rotation combination of the pan and tilt of the PTU. The calibration is based on the approach in Appendix D in [3].

The procedure captures images for different combinations of the Pan-Tilt unit , which are used to calibrate the camera with respect to a baseline position (pan=0, tilt=0). This gives us the position of the camera coordinate system (rotation and translation) with respect to the baseline. Then, the DAVIS sensor is calibrated with respect to the center of the PTU unit, using all the rotations and translations computed previously for the different combinations. This is done formulating a minimization problem that is solved searching for the translation, and then solving for rotation. Then the rotation of the DAVIS sensor coordinate system is computed, using simple averaging. The details can be found in the paper. The code is also available in the Section Resources.

Generating 2D motion flow field

The image motion flow field is the projection of the velocities of 3D scene points onto the image plane. The 3D velocities relate the 3D points \textbf{P} = (X, Y, Z) and their instantaneous motion \textbf{\.{P}} = -\textbf{t} - \textbf{\textit{w}} \times \textbf{P}, using Longuet-Higgins and Prazdny's model [4]. The 3D instantaneous motion \textbf{\.{P}} is then obtained as the sum of the translational velocity \textbf{t}=(t_{1}, t_{2}, t_{3}) and the rotational velocity \textbf{\textit{w}}=(\textit{w}_{1}, \textit{w}_{2}, \textit{w}_{3}). Now, the equation that relates the velocity in the image plane (\textbf{u}, \textbf{v}) with the 2D coordinates in the image plane (x,y), the 3D translation and 3D rotation, and the depth \textbf{Z} is

Citation

@article{barranco_dataset_2015,
	author = {Barranco, F. and Fermuller, C. and Aloimonos, Y. and Delbruck, T.},
	title = "A Dataset for Visual Navigation with Neuromorphic Methods",
	journal = "Frontiers in Neuroscience",
	year = "2015",
	month= "Nov.",
}

Resources

• Paper
• Complete dataset
• Matlab code available at a repository in GitHub.

References

Update Oct. 2016

Acknowledgements

Questions? Please contact fbarranco "at" ugr dot es